Sekä luonnossa että yhteiskunta- ja talouselämässä esiintyvät ilmiöt ovat luonteeltaan usein dynaamisia systeemejä: ne voidaan esittää peräkkäisinä ajan suhteen etenevinä tiloina. Systeemin tila tietyllä hetkellä yhdessä systeemin kehitykseen liittyvien lainalaisuuksien kanssa määrää systeemin tilan seuraavalla hetkellä. Niinpä esimerkiksi vallitsevalla säätilalla on suuri vaikutus odotettavissa olevaan huomiseen säähän, kaupunkien ja kuntien tulevien väestömäärien keskeisenä perustana ovat nykyiset väestömäärät jne.
Tällaisia systeemejä voidaan usein kuvata yksinkertaisilla matemaattisilla malleilla, joissa on vain yksi tai muutama muuttuja ja näiden muutosta kuvaavat epälineaariset yhtälöt. Jos malli on herkkä systeemin alkutilalle, sitä sanotaan kaoottiseksi. Kaoottisen mallin perusominaisuutena onkin levottomuus: havaittava käyttäytyminen on epäsäännöllistä ja jo erittäin pienet lähtöarvojen muutokset aikaansaavat käyttäytymisen täydellisen muuttumisen. Tästä huolimatta kyse on matemaattisesti kurinalaisesta mallista. Arkikielen tapaista negatiivista arvonväritystä ei matemaattiseen kaaokseen liity.

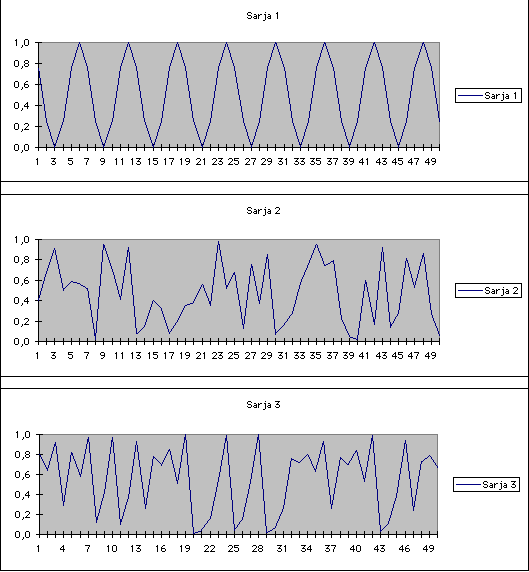
Kuvio 1. Dynaamisten systeemien kolme eri lajia
(1) xt = a· xt-1.
Mikäli esimerkiksi bakteeripopulaatio aina kaksinkertaistuu aikayksikössä, on a = 2 kaavassa (1). Tilillä 5%:n korkoa kasvavan pääoman karttumista kuvaava malli taas saadaan, kun asetetaan a = 1.05. Yksinkertainen kasvumalli johtaa rajoittamattomaan eksponentiaaliseen kasvuun (x0 on systeemin tila hetkellä t = 0 ):
(2) xt = x0·at.
Rajaton kasvu ei kuitenkaan ole juuri koskaan käytännössä mahdollinen. Belgialainen matemaatikko Pierre Verhulst kehitti n. 150 vuotta sitten matemaattisen mallin, jossa kasvun rajallisuus on yksinkertaisella tavalla otettu huomioon. Verhulstin logistisen kasvumallin dynamiikkaa kuvaa yhtälö
(3) xt = a· xt-1 ·(1-xt-1).
Systeemin tilaan liittyvä mittayksikkö on (3):ssa normitettu niin, että systeemin tilan maksimiarvo = 1. Malliin (1) verrattuna malliin (3) on tullut žkorjaustekijäksiÓ lauseke (1-xt-1), joka huolehtii siitä, että kun systeemin tila lähestyy maksimiarvoaan 1, samanaikaisesti pienenevä tekijä (1-xt-1) pitää kasvun kurissa.
Mallia (3) ei voida ratkaista analyyttisesti mallin (1) tapaan, on tyydyttävä
numeeriseen ratkaisuun iteroimalla. Tämä käy helposti esimerkiksi
taulukkolaskentaohjelmalla tai jopa laskimella. Jos annetaan kasvukertoimelle
a esimerkiksi arvo 1.5, saadaan alkutiloja x0 = 0.2, 0.4 ja
0.7 vastaavat taulukon 1 kehitysurat.
Taulukko 1. Logistisen mallin tasapainoratkaisut eri alkuarvoilla
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Taulukosta 1 käy selvästi ilmi tulos, jonka mukaan käyttäytymislakia (3) noudattava systeemi saavuttaa alkutilastaan riippumatta aina saman tasapainotilan (=1/3), kun kasvukerroin a = 1.5. Systeemin sanotaan olevan stabiili. Voidaan osoittaa, että tämä tilanne on voimassa kaikilla kasvukertoimen arvoilla välillä 0 < a < 3 (saavutettava tasapainotila luonnollisesti riippuu a:n arvosta).
Kun kasvukerroin ylittää arvon 3, muuttuu systeemin käyttäytyminen ratkaisevasti. Kiinteän tasapainotilan saavuttamisen sijasta systeemistä tulee jaksollinen: tasapainoratkaisu hyppii kahden eri arvon välillä. Kasvukertoimen arvolla a = 3 systeemillä on bifurkaatiopiste. Mikäli a:ta edelleen kasvatetaan, tapahtuu arvolla a = 3.45 uusi bifurkaatio, jakson kahdentuminen uudelleen: tasapainoratkaisussa toistuvat neljä eri tilaa säännöllisinä peräkkäin.
Nämä jakson kahdentumiset jatkuvat tihenevästi, kunnes arvolla a = 3.6 systeemin käyttäytyminen muuttuu kaoottiseksi, siis kuviossa 1 esitetyn sarjan 3 kaltaiseksi (kuviossa 1 on a = 4). Kaoottinen alue 3.6 < a < 4 (logistisen funktion määrittely-yhtälö on tulkinnallisesti järkevä vain alueella 0 < a < 4) ei ole kuitenkaan yhtenäinen, välillä on mm. sellaisia jaksollisen käyttäytymisen alueita, joissa jaksoina ovat 3 ja sen kerrannaiset.
Systeemin tasapainoratkaisun muodostamaa pistejoukkoa kutsutaan attraktoriksi. Kaoottisella systeemillä attraktorin muodostava pistejoukko on ääretön. Sitä kutsutaan oudoksi attraktoriksi.
Laitoksella valmistui v. 1997 kaksi tohtorin väitöskirjaa, joissa molemmissa aiheena oli kaaos-teoria tai sen lähialue. Irma Luhdan väitöskirja (Luhta 1997) oli kaaos-teoreettinen sovellus markkinointiin, Matti Laaksosen työn (Laaksonen 1997) aiheena taas olivat kansantalouden suhdannevaihtelut.
Mallin dynamiikan formulointi perustuu olettamukseen markkinoiden kolmesta vaihtoehtoisesta käyttäytymismuodosta. Yksinkertaisin vaihtoehto on, että markka mainontaan lisää yrityksen googwilliä yhdellä yksiköllä. Tälläinen lineaarinen yhteys jättää kuitenkin huomiotta ns. unohtamisefektin eli markka mainontaan saattaakin lisätä goodwilliä tietyn ajan kuluttua ykköstä pienemmällä määrällä eli mainonnan rajahyöty on vähenevä. Kolmanneksi voidaan ajatella, että goodwillillä on jokin saturaatiotaso, jota ei voida ylittää millään mainonnan määrällä.
Yrityksen kannalta on tärkeää, että systeemin tasapainogoodwill on stabiili, jotta yritys pystyy arvioimaan goodwilliänsä ja suunnittelemaan siihen johtavaa mainontapolitiikkaa. Mallissa epästabiilisuus johtaa joko suoraan jakson kahdentumisbifurkaatioiden (mainonnalla välitön vaikutus) tai Hopfin bifurkaatioiden (mainonnalla viivästetty vaikutus) kautta kaaokseen mallin parametrien muuttuessa yrityksen kannalta epäsuotuisaan suuntaan (esim. goodwillin kulumisnopeus kasvaa). Hopfin bifurkaatiossa tapahtuu repellointi-ilmiö eli yrityksen goodwill alkaa heilahdella syklisesti. Tilanne on kuitenkin rakenteellisesti stabiili ja tulkinnallisesti mielekäs taloudellisten ilmiöiden syklisyyden perusteella.
Luhdan tutkimuksessa on kehitetty laaja diagnostinen välineistö mallin kvalitatiivisen käyttäytymisen ja rakenteellisten muutosten kuvaamiseen numeerisesti ja graafisesti. Käytettyjä kaaosteorian menetelmiä ovat yksi- ja kaksiulotteiset bifurkaatiodiagrammit, Lyapunovin eksponentit sekä korrelaatiodimensio-tekniikat. Analyysit perustuvat simulaatio-ohjelmiin, joista erityisesti värikkäät bifurkaatiokuvat ovat uusi väline dynaamisen mallin käyttäytymisen visualisoinnissa.
Väitöskirjan jatkotutkimuksessa malliin on tarkoitus lisätä uusia muuttujia, esimerkiksi verotus, jolloin malli voi saada myös kaoottisia käyttäytymismuotoja. Verotuksella täydennetty kansantulomalli voi esimerkiksi auttaa arvioimaan kansantuloa tai verokertymää eri suhdannevaiheissa tai eri voimakkuuksisten suhdanteiden vallitessa. Tässä yhteydessä kaaokseen ei liity, kuten ei kaaos-teoriassa yleensäkään, mitään suurta dramatiikkaa tai katastrofaalisuutta. Matemaattisessa mielessä kaaos merkitsee vain tietynlaista havainnoitsijalle näkyvää epäsäännöllisyyttä, jonka kulkua hallitsevat kuitenkin selvät lainalaisuudet.
Kangasaho J., Mäkinen J., Oikkonen J., Paasonen J. & Salmela M. (1996). Numeerinen matematiikka. Porvoo: WSOY.
Laaksonen M. (1997). A nice portrait of restless systems - Uniqueness of the limit cycle of some Liénard equations. Acta Wasaensia, No 57.
Luhta I. (1997). Structural changes in a complex system: a chaos-analytic
study of a nonlinear advertising policy. Acta Wasaensia, No
52.